منیفولدها: پایهایترین مفهوم در ریاضیات مدرن و کاربردهای آن
منیفولد چیست؟ — تعریف ساده، انواع و کاربردهای واقعی در فیزیک و هوش مصنوعی
منیفولدها (Manifolds) یکی از بنیادیترین مفاهیم در ریاضیات مدرن هستند که امکان مدلسازی فضاهای پیچیده را فراهم میکنند. این ساختارها فضاهایی را توصیف میکنند که محلی شبیه به فضای اقلیدسی (مانند خط، صفحه یا فضای سهبعدی) رفتار میکنند، اما در مقیاس کلی میتوانند شکلهای بسیار پیچیدهای داشته باشند. امروزه، منیفولدها در رشتههای مختلفی مانند فیزیک، علوم کامپیوتر، رباتیک، گرافیک کامپیوتری و یادگیری ماشین نقش کلیدی ایفا میکنند. اگر دانشجوی ریاضی، فیزیک یا مهندسی هستید، درک این مفهوم میتواند دریچهای به دنیای پیشرفتهتر علوم باز کند.
در این مقاله، به بررسی تعریف منیفولد، انواع آن، ویژگیهای کلیدی، کاربردها و اهمیت یادگیری آن میپردازیم. هدف این است که این مفهوم پیچیده را به زبانی ساده و قابل فهم برای دانشجویان توضیح دهیم.
منیفولد چیست؟ (تعریف ساده و دقیق)
منیفولد یک فضای توپولوژیکی Hausdorff، شمارنده دوم (second-countable) و محلی اقلیدسی با بعد ثابت است. به عبارت سادهتر:
- به صورت محلی شبیه فضای اقلیدسی رفتار میکند: یعنی هر نقطه روی منیفولد، اطرافش شبیه یک فضای صاف و معمولی (مانند صفحه یا خط) است. مثلاً سطح یک کره از نزدیک شبیه یک صفحه مسطح به نظر میرسد.
- ساختار کلی آن میتواند پیچیده باشد: اما وقتی از دور نگاه کنید، ممکن است خمیده، سوراخدار یا چندبعدی باشد.
به زبان روزمره: تصور کنید روی یک بخش کوچک از منیفولد زوم کنید؛ آن قسمت کاملاً صاف و ساده به نظر میرسد. اما وقتی کل ساختار را ببینید، ممکن است پیچوتابهای جالبی داشته باشد.
مثال ملموس: سطح زمین یک منیفولد دوبعدی است. محلی (مثلاً در یک شهر) صاف به نظر میرسد، اما منحنی و کروی است.
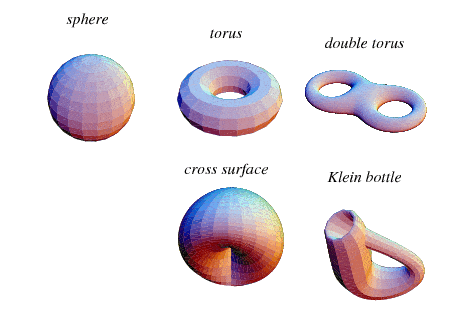
انواع منیفولدها
منیفولدها بر اساس ساختار ریاضی تعریفشده روی آنها دستهبندی میشوند. در ادامه، مهمترین انواع را بررسی میکنیم:
- منیفولد توپولوژیکی (Topological Manifold) سادهترین نوع منیفولد است که فقط از منظر پیوستگی و همارزی توپولوژیکی بررسی میشود. در این نوع، تمرکز روی خواصی مانند اتصال و سوراخدار بودن است، بدون توجه به مشتق یا انحنا.
- منیفولد دیفرانسیلی یا صاف (Smooth Manifold) منیفولدی که ساختار دیفرانسیلپذیر (معمولاً C∞) روی آن تعریف شده است، یعنی تغییر مختصات بین چارتها (نقشههای محلی) توابع صاف هستند. این نوع پایه اصلی هندسه دیفرانسیل، فیزیک نظری و نسبیت عام است.
- منیفولدهای پیچیده (Complex Manifolds) مختصات آنها با اعداد مختلط تعریف میشود. این منیفولدها در هندسه جبری، نظریه ریسمان و ریاضیات پیشرفته کاربرد دارند.
نکته اضافی: منیفولدها میتوانند با مرز (مانند دیسک) یا بدون مرز (مانند کره) باشند و همچنین باز یا بسته.
ویژگیهای کلیدی منیفولدها
برای درک بهتر منیفولدها، به ویژگیهای اصلی آنها توجه کنید:
- بُعد (Dimension) تعداد مختصات لازم برای مشخص کردن یک نقطه روی منیفولد. مثالها:
- خط: یکبعدی
- صفحه: دوبعدی
- سطح کره: دوبعدی (هرچند در فضای سهبعدی قرار دارد؛ فقط دو مختصه مانند عرض و طول جغرافیایی نیاز دارد)
- فضا-زمان در فیزیک: چهاربعدی (سه بعد فضایی + یک بعد زمانی)
- توپولوژی (Topology) نحوه اتصال و پیوستگی فضا. این ویژگی تغییرناپذیر تحت کشش یا خم کردن است (بدون پاره کردن یا چسباندن). مثال جالب: یک دونات (توروس) و یک فنجان قهوه از نظر توپولوژیکی یکسان هستند! هر دو یک سوراخ دارند (جنس = ۱). این مفهوم به “همدیفرانسی توپولوژیکی” معروف است.
- انحنا (Curvature) اندازهگیری میزان انحراف فضا از حالت صاف. انحنای مثبت (مانند کره)، منفی (مانند زین اسب) یا صفر (مانند صفحه) وجود دارد. در نسبیت عام، انحنا همان گرانش است.
کاربردهای منیفولدها در علوم مختلف
منیفولدها فراتر از ریاضیات محض، در دنیای واقعی کاربردهای گستردهای دارند:
- فیزیک – نسبیت عام در نظریه آلبرت انیشتین، فضا-زمان یک منیفولد چهاربعدی منحنی است. جرم و انرژی این منیفولد را خم میکنند و این خمیدگی را ما به عنوان نیروی گرانش تجربه میکنیم.
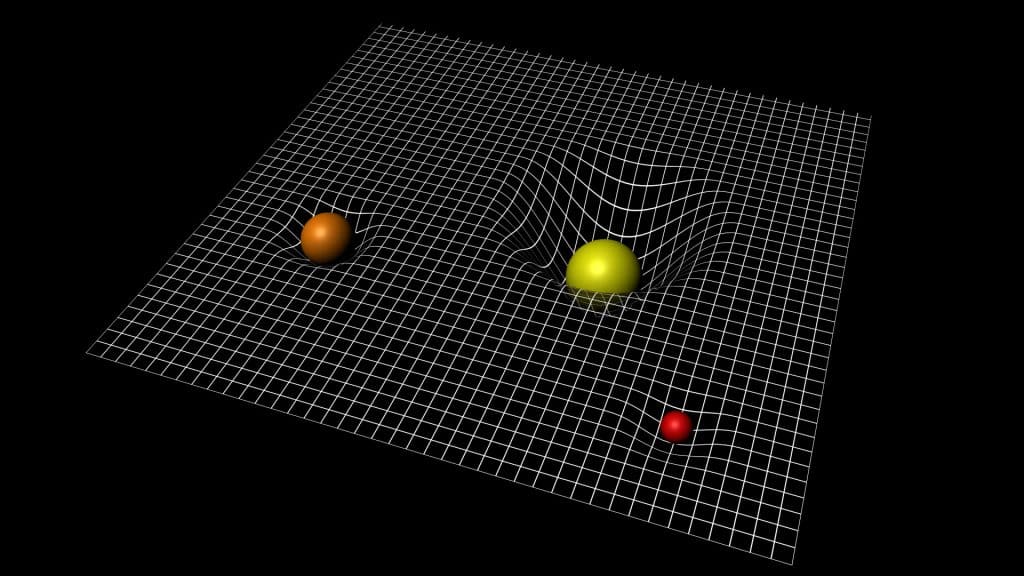
- رباتیک – مدلسازی حرکت حالتهای یک ربات (زاویه مفاصل، موقعیت) یک فضای چندبعدی تشکیل میدهند که اغلب یک منیفولد دیفرانسیلی است. این مدلسازی برای کنترل رباتهای صنعتی یا humanoid ضروری است.
- علوم کامپیوتر – یادگیری ماشین و Manifold Hypothesis فرضیه معروف Manifold Hypothesis میگوید دادههای واقعی (مانند تصاویر یا متن) روی یک منیفولد کمبعدی در فضای پربعدی قرار دارند. این ایده پایه روشهایی مانند t-SNE، UMAP، Autoencoderها و حتی Transformerها است که سعی میکنند این ساختار پنهان را کشف کنند.
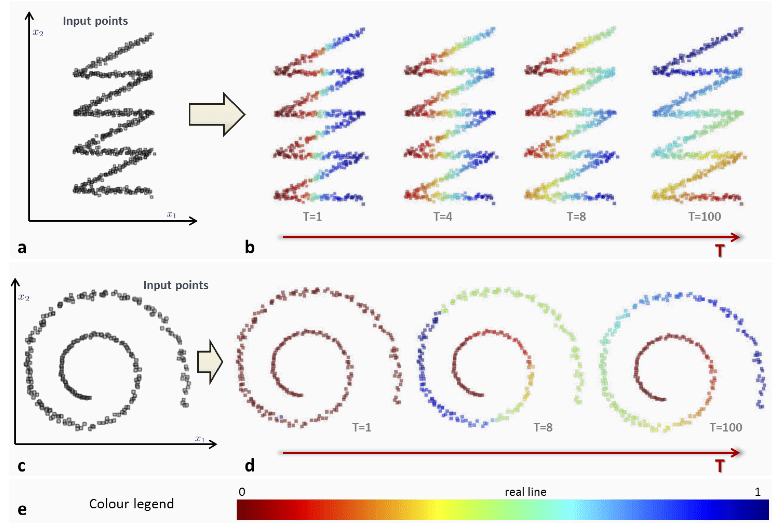
- گرافیک کامپیوتری مدلهای سهبعدی (مانند شخصیتهای بازی یا اجسام در انیمیشن) اغلب به عنوان منیفولدهای دوبعدی (سطوح خمیده) تعریف میشوند. مثلاً در نرمافزارهایی مانند Blender یا Maya، مشهای triangular تقریب گسستهای از این منیفولدها هستند.
- مهندسی – تحلیل اجسام صنعتی سطوح دوبعدی اجسام مانند بدنه هواپیما یا دیسک ترمز خودرو در نرمافزارهایی مانند CATIA یا SolidWorks به عنوان منیفولدهای پارامتریک (مانند NURBS) مدلسازی میشوند. این مدلها برای تحلیل تنش، ارتعاش یا حرارت استفاده میشوند.
چرا یادگیری منیفولدها برای دانشجویان مهم است؟
- زبان اصلی فیزیک مدرن: درک نسبیت، مکانیک کوانتومی و نظریه میدانها بدون منیفولدها ممکن نیست.
- ابزار هندسه پیشرفته: پایهای برای هندسه دیفرانسیل و توپولوژی.
- پایه علمی هوش مصنوعی: در یادگیری عمیق و پردازش دادههای بزرگ.
- کاربرد در مهندسی: از رباتیک و کنترل تا پردازش تصویر و بینایی ماشین.
- درک بهتر دنیای واقعی: کمک به مدلسازی فضاهای پیچیده و دادههای عظیم.
اگر دانشجو هستید، پیشنهاد میکنم با کتابهایی مانند “Introduction to Smooth Manifolds” نوشته John M. Lee شروع کنید یا ویدئوهای آموزشی در یوتیوب جستجو کنید.
جمعبندی
منیفولدها پلی شگفتانگیز بین هندسه ساده روزمره و پیچیدگیهای دنیای واقعی هستند. از خمیدگی فضا-زمان در نظریه انیشتین تا حرکت رباتهای چنددرجه آزادی، از مدلهای سهبعدی در بازی و سینما تا کشف ساختار پنهان میلیونها داده در هوش مصنوعی — همه اینها در قالب منیفولدها قابل تحلیلاند. یادگیری این مفهوم نه تنها دانش شما را عمیقتر میکند، بلکه به شما کمک میکند مسائل واقعی را بهتر حل کنید.
اگر سؤالی دارید یا میخواهید مثالهای بیشتری ببینید، در کامنتها بنویسید!
متا متریال های مکانیکی یا مواد با نسبت منفی پواسون
کتابخانه مثال های نرم افزار کامسول
برنامه محاسبه مقاومت معادل با زبان های فرترن، جاوا و ++C
کانال اطلاع رسانی تیم علمی و آموزشی دایا
دیدگاهتان را بنویسید